Before going to the program first let us understand what is a Quadratic Equation?
Quadratic Equation:
A Quadratic Equation is any equation having the form: 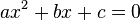
where x represents an unknown, and a, b, and c represent known numbers such that a is not equal to 0. If a = 0, then the equation is linear equation, not quadratic.
For Example,
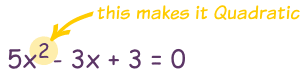
For more understanding you can check out the following link:
https://www.mathsisfun.com/algebra/quadratic-equation.html
Program code to find roots of Quadratic Equation:
#include <stdio.h>
#include<conio.h>
#include <math.h>
void main()
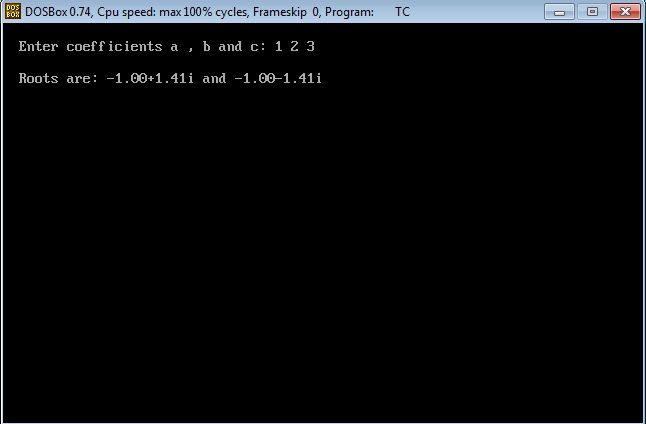
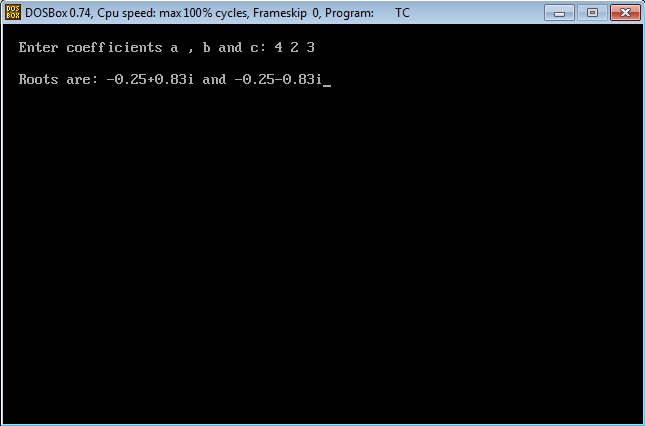
{ float a, b, c, determinant, r1,r2, real, imag; clrscr(); printf("Enter coefficients a, b and c: "); scanf("%f%f%f",&a,&b,&c); determinant=b*b-4*a*c; if (determinant>0) { r1= (-b+sqrt(determinant))/(2*a); r2= (-b-sqrt(determinant))/(2*a); printf("Roots are: %.2f and %.2f",r1 , r2); } else if (determinant==0) { r1 = r2 = -b/(2*a); printf("Roots are: %.2f and %.2f", r1, r2); } else { real= -b/(2*a); imag = sqrt(-determinant)/(2*a); printf("Roots are: %.2f+%.2fi and %.2f-%.2fi", real, imag, real, imag); } getch();
}
Step by Step working of the above Program Code:
- First the computer reads the coefficients a , b and c from the user.
- Then it computes the value of determinant using the formula.
determinant=b*b-4*a*c;
- Then checks the determinant value is greater than , equal or less than to zero using if else if ladder.
- If the determinant value is greater than zero, then root1 and root2 value is calculated using the formula:
r1=(-b+sqrt(determinant))/(2*a)
r2=(-b-sqrt(determinant))/(2*a)
- If the determinant value is equal to zero, then root1 and root2 value is calculated using the formula:
r1=r2=-b/(2*a)
- If the determinant value is less than zero, then root1 and root2 value is calculated using the formula:
real=-b/(2*a)
imag=sqrt(-determinant)/(2*a)
- Finally print the roots of the quadratic equation.
Output: