C++ program for Sine Series

Before going to the program for Sine Series first let us understand what is a Sine Series?

Sine Series:

                Sine Series is a series which is used to find the value of Sin(x).

where, x is the angle in degree which is converted to Radian.

The formula used to express the Sin(x) as Sine Series is

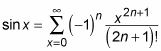
Expanding the above notation, the formula of Sine Series is

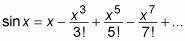
For example,

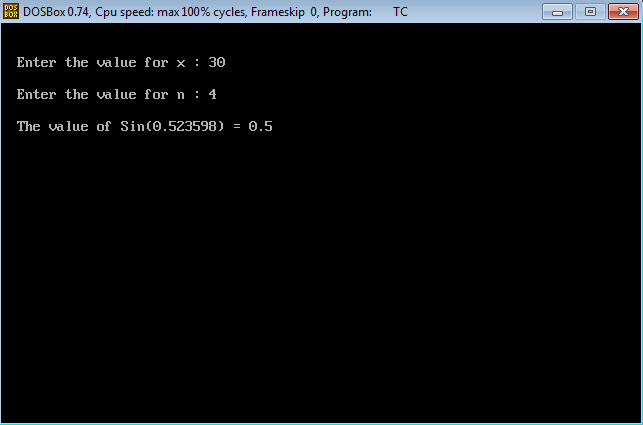
                Let the value of x be 30.

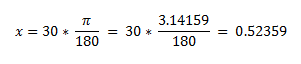
So, Radian value for 30 degree is 0.52359.

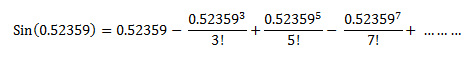
So, the value of Sin(30) is 0.5.

Program code for Sine Series in C++:

#include<iostream.h>
#include<iomanip.h>
#include<conio.h> void main()
{ int i, n; float x, sum, t; clrscr(); cout<<" Enter the value for x : "; cin>>x; cout<<" Enter the value for n : "; cin>>n; x=x*3.14159/180; t=x; sum=x; /* Loop to calculate the value of Sine */ for(i=1;i<=n;i++) { t=(t*(-1)*x*x)/(2*i*(2*i+1)); sum=sum+t; } cout<<" The value of Sin("<<x<<") = "<<setprecision(4)<<sum; getch();
}

Note: setprecision(4) is used to set the floating point number upto 4 decimal points.

     iomanip.h is a header file which contains the setprecision() function.

Related: C++ program for Cosine Series

Working:

• First the computer reads the value of  ‘x’ and ‘n’ from the user.
• Then ‘x’ is converted to radian value.
• Then using for loop the value of Sin(x) is calculate.
• Finally the value of Sin(x) is printed.

Related: C++ program for Exponential Series

Step by Step working of the above Program Code:

Let us assume that the user enters the value of ‘x’ as 30 and ‘n’ as 3.

1. Converting ‘x’ to radian value

x = x * 3.14159 / 180    (x = 30 * 3.14159 / 180)    So,  x=0.523598

2. It assigns t=x and sum=x (i.e. t=0.523598 and sum=0.523598)
3. It assigns the value of i=1 and the loop continues till the condition of the for loop is true.

3.1.   i<=n    (1<=3)    for loop condition is true

t = (0.523598 * (-1) * 0.523598 * 0.523598)/(2 * 1 * (2 * 1 + 1))

So,  t = – 0.02392

sum = 0.52359 + (- 0.02392)

So,  sum=0.499678

i++

So,  i=2

3.2.   i<=n    (2<=3)    for loop condition is true

t = (- 0.0239 * (-1) * 0.523598 * 0.523598)/(2 * 2 * (2 * 2 + 1))

So,  t = 0.000327

sum = 0.499678 + 0.000327

So,  sum=0.500005

i++

So,  i=3

3.3.   i<=n    (3<=3)    for loop condition is true

t = (0.000327 * (-1) * 0.523598 * 0.523598)/(2 * 3 * (2 * 3 + 1))

So,  t = – 0.000002

sum = 0.500005 + (- 0.000002)

So,  sum=0.500003

i++

So,  i=4

3.4.  i<=n    (4<=3)    for loop condition is false

It comes out of the for loop.

4. Finally it prints The value of  Sin(0.523598) = 0.5

5. Thus program execution is completed.

Output:

TO DOWNLOAD THE PROGRAM CODE : CLICK HERE